Improving Literacy in Maths

I've been thinking, lately, about how to improve literacy in Maths. If you would like to read the strategies I have so far come up with, skip to the first heading.

For the first time this year I am teaching Functional Skills Mathematics (Levels 1 and 2). The scheme of work I have for these classes is pretty bare-bones and is very skills-based. I am finding it hard to stick straight to the scheme of work, as most of these skills are actually more basic than what my students have already seen when attempting their GCSE and are made even simpler as there is no non-calculator test.

Historically, many students fail the level 2 course and when I asked my colleagues why, they all said that it was down to poor literacy skills. This is understandable when the questions all look like this:

 

Obviously literacy isn't the only difficulty with this question, so I have decided to teach Functional Skills with a four-pronged approach. I will go in to detail about the other prongs of my plan in a separate post... Prongs.

Prong one: Ways to Improve Literacy

1. Scaffolding questions and correct working

This can be done in different ways.

• So far I have been getting them to write titles for each seperate part of their working before starting any calculations, so that they can then split the work in to more managable chunks.
• In future I will try using a problem scafforlding sheet like this:

• Problems with clue cards would also help to split up a question and promote discussion and team-work. It works like this: Each group gets a simple question. Each individual in the group also gets a different card with a single piece of information that is needed to answer the main question. Members of the group have to decide how to use and combine the information sheets they are given. Here is an example (For lots more, click here):

• Question sequencing: All the correct working for a set of problems is written down on separate tabs of paper, but their order has been mixed up. Students must put the working in to a correct order.

2. Building vocabulary and making connections

This could include:

• Word-walls: Where mathematical words can be written with their definitions and/or diagrams and grouped according to connections with other words.
• Connect-two: You have a list of words at the top (eg. Percentage, fraction, TAX, Chocolate). You pick different pairs of them and explain in what way they are connected and give examples.
• Word-splash: Similar to connect-two, but the words are on the board and you pick people to make a connection.
• Anticipation guide: A table where the first column consists of statments and/or questions (eg. A decimal number is a number less than 1). The second and third columns give a space where students decide whether they think the statement is true or false and why. The second column gets their opinions before working on the subject and the third column gets it after working on the subject (good evidence of progression here too!).
• Tarsias: These are jigsaws where students match a question to an answer (or a word to its definition). Mr Barton has loads available here. You could also print off a blank tarsia and get students to create one.
• 3 facts and a fib: Students write down three facts and a lie about a maths object, word or topic. They try to make the lie believable enough that when they pass it to their neighbour, the neighbour can not work out which statement is the lie.
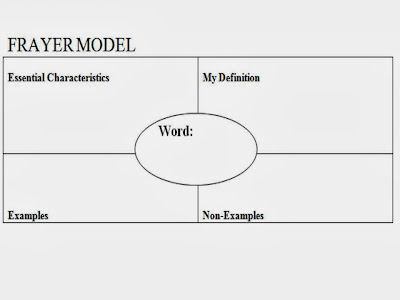
• Definition map: to the example below I would add a space for illustrations of the word or concept:
  
  
• Taboo: The classic game game be adapted easily to a nice plenary activity - give them a maths password (eg. Mutually-exclusive) and a list of taboo words that they are not allowed to use (eg. Probability, events, same time, both). The chosen student then has to describe the password, without using any taboo words, to the class until someone can guess it.
• Pictionary: Similar to taboo except that you make drawings to represent the word.
• The Mathematics Assessment Project has many matching activities designed to promote discussions and expose misconceptions, as well as Professional Development modules to help you use them effectively. Some of them are excellent.
• Think, pair, share: Students work on their own on a question. In this time they may do some calculations but should focus more on organising the information and making notes. Next they get in to pairs. First they should take it in turns explaining their thoughts (one talker, one listener) so far, before working together to answer the question. Finally, they join another group and explain how they got to their answer (again taking it in turns so that both groups get to explain their work).
• Odd one out: Take three different mathematical objects (eg. triangles) and get students to decide which is the odd one out, then discuss their decision with their partner. This works best if each object could be the odd one out for a different reason (isoceles, right-angled, different area, different perimeter, etc.). That way different students get a different answer and their discussions lead others to see the objects in another way.
• Carroll diagrams: Two-way tables where students have to sort objects in to the correct section that matches the description of that word. Here is a good example.

3. Peer marking and constructive discussion

• Marking each others' work will help them understand the improtance of clear working, with titles, explanations,etc. Discussing how a correct answer could be improved to make it more clear would also help with this.
• Always, sometimes, never true: Students read a statement and decide whether it is always true, never true, or sometimes true. They then justify their answer and compare results with their peers (examples can be found here).
• Rally coaching -  Students work in pairs. They take it in turns with one person answering a single question, whilst the other coaches. Coaching could simply be helping to solve the questions or could be more complex, with rules like, "avoid telling them what to do. Try to ask a question that will help them to figure out the next step."
• Many of the activities from section 2 would also apply here.
• Bowland Maths have a Professional Devolopment activity (module 3) described as "Fostering and Managing Collaborative Work: How can I get them to stop talking and start discussing?" I have not been able to look at this yet  as there is no sound on my computer at school, but I will update the page when I do. I have already enjoyed and would recommend some of the other PD modules on this site though.

4. Filtering information from text

• Students highlight the different parts of a question in different colours (question, given figures, constraints, etc.)
• Students write the gist of a block of text using only 20 words. Students could create an individual version, then a version in pairs, before writing a final one in their books.
• There is a video series (click here) with worksheets (click here for the worksheets), where you are asked to fill in information as you hear it on the videos.

Credits

Much of these ideas (and plenty more ideas!) have come from:

• "Growing the Connection Between Mathematics and Best-Practice Reading and Writing Strategies" by Jennifer Kosiak, Sue Schumann, Ann Harry and Bonnie Jancik (available here)
• "WHAT’S LITERACY GOT TO DO WITH IT? Literacy in the Math and Science Classroom" by Blair Covino and Barb Mazzolini  (available here)
• "Literacy in Maths" by The Highland Curriculum for Excellence (available here)
• Other sources that have been linked above: Cumbria Grid for Learning, Mr Barton, Mathematics Assessment Project, Nrich, Bowland Maths and Channel 4 Learning.