Principles of Engelmann's Direct Instruction: Atomisation

This post is part of a series where I go in to detail on some of the main aspects of Direct Instruction as laid out by Siegfried Engelmann in this book.

Below are links to the other posts in this series. Scroll past them to read the article.

• Atomisation
• Overtisation
• Expansion and Context Shaping
• Cognitive load
• Review
• Lesson structure and schemes of work
• Speed principle
• Difficulty and Motivation
• Defining range/scope
• Categories for different types of knowledge
• Instruction for basic types of knowledge and fact systems
• Instruction for linked types of knowledge
• Instruction for routines
• Instruction for problem solving techniques
• "Real world" maths
• Prompts and scaffolding
• Correcting mistakes
• My take on the strengths and weaknesses of Direct Instruction

Atomisation

Atomisation, to me, is the part of Direct Instruction that I found both the easiest to implement and the most impactful in terms of student outcomes. It is the splitting up of a skill or topic in to its indivisible component pieces of knowledge. It is important that these components each have a overt, assessable outcome (more on this in overtisation).

Each component skill can then be categorised and taught separately before being put together to learn the target skill or topic. There are several advantages to doing this:

1. It reduces cognitive load as students only have to concentrate on one aspect at a time.
2. It is easier to correct mistakes as there is only one component for students to misunderstand.
3. With a narrower focus to the topic, students can explore the full range of this component quickly. This means that they are more likely to get a deep understanding of the component.
4. It allows for a high percentage of student successes, building confidence in their abilities.
5. It gives you, as a teacher, a better understanding of how difficult a topic will be for students.
6. It helps to avoid stipulation, the learning of misrules about a topic.
7. It makes behaviour management easier.

Example:

Let's take a look at right-angled trigonometry:

In the past, I would probably still have done some splitting up of this topic in to smaller parts. Perhaps by working on missing angles before missing sides, or by looking at only sin before cos and tan. However, I don't think I really understood how complicated trigonometry can be until I atomised it. This is how I would split up the components of basic trig:

• Deciding when trigonometry can/should be used
• Deciding which equation to use
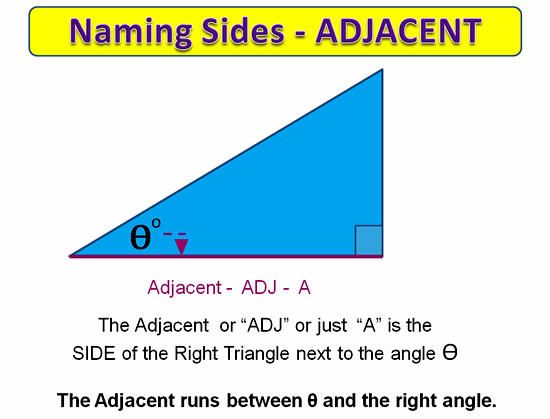
• Labelling the sides of triangles as opp, adj, hyp 
• Remembering the three trigonometry triangles
• Write down 9 equations from the three trigonometry triangles
• Using compound measure triangles to create equations
• Solving the equation
• Substituting values in to a formula
• Using algebra as a variable
• Solving one-step equations involving inverse trig functions
• Applying inverse functions to a fraction
• Using algebra as an unknown
• Using the trig and inverse trig buttons on a calculator
• Combining the above steps in a clear routine

Now let's look at how this affects each of the advantages above.

1. Imagine the cognitive load of weaker students trying to process all that at the same time!
2. Students may have a misconception about any one of these components. This misconception may only occur for certain types of questions and it may not be visibly shown in their working. This makes it very difficult to diagnose mistakes. However, if you are only teaching how to "Write down 9 equations from the three trigonometry triangles", you minimise the number of different misconceptions students can have (either they get the order wrong or they mess up the sin(angle) part).
3. In the past, I may have scaffolded trig for my students by looking at an easy subset of the problems (e.g. only sin, only finding hypotenuse). This can easily lead to students learning cognitive shortcuts that do not work for all questions. Another common difficulty with trig is the relative nature of opposite and adjacent sides (the fact that these switch when seen from the perspective of different angles). However, if you teach "Labelling the sides of triangles as opp, adj, hyp" as a separate skill, you can explicitly show all variations of this and students can practice and be assessed on it in depth in a matter of minutes.
4. Before, I have despaired at the thought of teaching trig to a lower ability class! In the past I might have tried whilst only expecting 50-60% of students to succeed (cementing students' self-images of low intelligence) or skipped the topic altogether. However, atomisation gives me a route map to build up their knowledge whilst ensuring the success of >95% of the class on each component.
5. I now have a much more detailed idea of how difficult the topic will be for students and the potential pitfalls they may have. Combined with my knowledge of the class, I can decide for each component whether they need to be assessed, recapped with review activities/homework or completely retaught/taught from scratch.
6. Stipulation, or the learning of misrules, can be very difficult to remedy once embedded in to their practice. As mentioned in point 2, atomisation helps to spot and correct these misunderstandings during initial instruction.
7. Teaching trig is complex. To explain it takes at least 5 minutes, even without students' questions and other interruptions. Getting 5 minutes of undivided attention from some classes is a big ask. However, all of the components listed can be explained in under 1 minute. I have found that students are much more willing to give you their attention when you ask for it in short, efficient bursts like this.

Unanswered questions:

Here are a few reflections I have had about atomisation that I still do not have an answer to:

• Is it ok to combine components sometimes in order to speed up the teaching of a topic? 
• When is it ok to combine components? 
• With which types of components is it ok to combine them?
• How different would this look with different classes?

Other practicalities:

It is important to show the full range of possible questions that can be asked of any particular atom to avoid students learning cognitive shortcuts. These shortcuts can cause serious problems if embedded in their learning as they can be very difficult to unlearn.

If you cannot teach the full range of possible questions in a single session, you should still show the full range, with students marking off the questions that "we don't know how to do yet".